Problems and Solutions
Some texts will go here at a later time ...
General Problems
The problems of this section might seem simple and irrelevant but, they are designed to test the problem solving skills of engineering students. Each problem tests a number of important aspects that engineers should be aware of. Similar challenges in different forms may face engineers in solving design problems.
Problem 1: the nine-dot
You have nine dots arranged as in the figure below. The task is to connect the lines with only four, consecutive, straight lines without retracing or taking the pen/pencil off the paper.
 |
| The nine-dot problem |
Solution:
Our mind subconsciously draws an invisible boundary for the problem that limits our ability to solve it. The figure below shows the dots with invisible boundary.
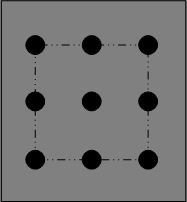 |
| Subconsciously drawn, invisible boundary |
To successfully solve the problem, we have to think beyond that boundary. The figure below shows a solution for this problem.
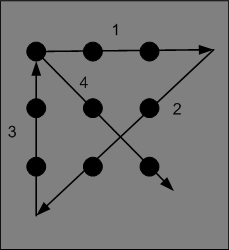 |
| Solution of the nine-dot problem |
return top
Problem 2: the six-matchstick problem
You have to arrange six matchsticks to form four equilateral triangles. You are not allowed to break the sticks.
Solution:
Like problem 1, the mind again draws an invisible boundary for the problem. This time, the boundary limits us to think in only two dimensions. We have to think in three dimensions in order to solve this problem. Figure below depicts the solution.
 |
| Solution of the six-matchstick problem |
return top
Problem 3: the 12-ball
You have 12 spherical, similar balls. One of the balls is either heavier or lighter than the others. The other balls are all with the same weight. You have to identify the odd ball using a balance. The only rule is that you can only use the balance 4 times.
Solution:
This problem requires trial and error method to solve. But the basic idea is to understand the problem and its key point. The key point is that we don’t know whether the ball is heavier or lighter. If we start weighing the balls in groups of 6, with 6 balls on each side of the balance, we will use up our 4 chances of using the balance without getting a result.
We divide the balls into three groups of 4 balls. We call them group A, B, and C. We set aside group A and weigh the other two groups, groups B and C, against each other. The balance will either be even or uneven. If it was even then the odd ball would be in group A. But we still don’t know if it was heavier or lighter yet. If the balance was uneven, then the odd ball is in either group B or C.
The balance is even:
Now we know the odd ball is in group A. At this point, we have 3 more chances to use the balance. We further divide group A into two groups each of 2 balls. We call them A1 and A2. We then weigh A1 against 2 balls from either group B or C. Again we have two cases: if the balance was even then the odd ball is in A2 but we still don’t know if it is lighter or heavier. Otherwise it is in A1 and the balance indicates whether it is lighter or heavier. In this case, we only need one more use of the balance to identify the ball. But in case the ball was in A2, we will have to set aside one ball and weigh the other against any balls form B or C. If the balance was even, we would know the ball is the one we set aside but still we will have to weigh it one more time to see if it is lighter or heavier.
Above is how we solve this problem. Other cases have to be examined the same way.
return top
Problem 4: the string and the room
You are in an empty room with two strings hanging from its ceiling, a chair, and a pair of pliers. You are asked to tie the ends of the strings together. The strings are fixed and cannot be moved. You cannot reach the strings without the use of the chair. Also, you can only reach one string using the chair. How do you tie the ends together?
Solution:
The pliers are the key to the solution of this problem. The key word is “swing”. We swing one end of a string using the pliers and catch it at the other end while on the chair. The idea is, while a pair of pliers can be used for grabbing and cutting wires, it can also be used for building a pendulum. Engineers must be able to imagine things beyond their boundaries.
return top
Problem 5: the chains
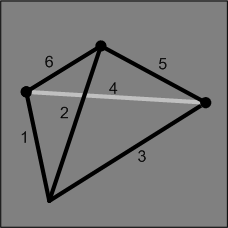
There are four chains each with three links. See the figure below. You are asked to join the chain together into one, closed, single chain. Opening a link cost 2 cents. But closing a link cost 3 cents. How do you join the chains so that the cost will not go higher than 15 cents?
 |
| Four chains each with three links |
Solution:
We open the three links of a chain. This will cost us 6 cents. Then we join the other three chains with the links we have. Joining will cost us 3 times closing which means 9 cents. The total cost will be 15 cents.
return top
Problem 6: The four careers
Roger, Laura, Brenda, and Mark work in the city as a singer, stockbroker, salesperson, and cook, but not necessarily in that order. The salesperson and the singer carpool with Laura. Mark plays tennis with the salesperson and the cook. The cook drives to work alone. Roger envies the salesperson. Which person has which career?
Solution:
The solution is already given in the problem explicitly. We only need to deduce the solution from the given facts:
- The salesperson and the singer carpool with Laura: this fact implies that Laura is neither the salesperson nor the singer
- Mark plays tennis with the salesperson and the cook: this implies that Mark is neither the salesperson nor the cook
- The cook drives to work alone: means that Laura is not the cook
- Roger envies the salesperson: implies that Roger is not the salesperson
From these facts we form a table like below:
| singer | stockbroker | salesperson | cook | |
| Roger | NO | NO | NO | YES |
| Laura | NO | YES | NO | NO |
| Brenda | NO | NO | YES | NO |
| Mark | YES | NO | NO | NO |
Roger is the cook, Laura is the stockbroker, Brenda is the salesperson, and Mark is the singer.
return top
Boolean Problems
Problem 1: use the Boolean theorems to simplify:
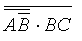 |
Solution:
First we should remember that complementation in Boolean algebra has precedence over multiplication which in turn has precedence over addition. Using de Morgan's theorem:
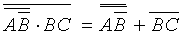 |
Two complements will cancel each other leaving:
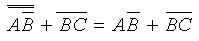 |
Applying de Morgan's theorem again:
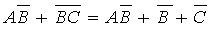 |
But AB + B is the same as B(A + 1) and A + 1 is equal to ‘1’ regardless of the value of A, then:
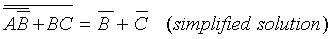 |
return top
Problem 2: prove that:
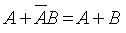 |
Solution:
We start analysing the variable A. And we find out that A+A is still A and, A+AB will also result in A since A is a common factor and B+1 is ‘1’. Below are the steps to prove the equation above:
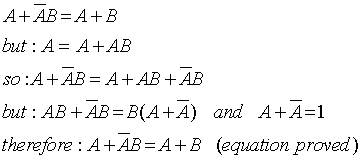 |
return top
Problem 3: simplify the Boolean expression:
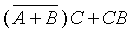 |
Solution:
We apply the de Morgan’s theorem on A+B:
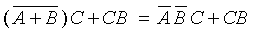 |
We then factor C out:
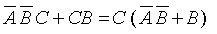 |
The expression C(A B+B) can be modified to:
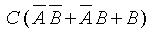 |
because the Boolean variable B can be expressed as AB+B since:
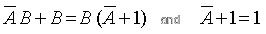 |
Then we can modify A B+AB and reduce it to a simpler expression like below:
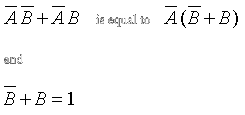 |
which results in just A. Now we have a new expression:
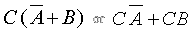 |
return top
Bit Manipulation Problems
Problem 1: shift the binary bits 10010111 to the left. Use arithmetic shift.
Solution:
We insert a ‘0’ bit from the right and move the other bits to the left. The left-most bit will be dropped or discarded.
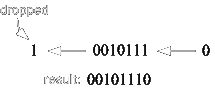 |
“ Note: logical shifting and rotating to the left are the same as arithmetic shifting to the left. This means that shifting and rotating to the left are the same. ”
return top
Problem 2: shift the binary bits 10010111 to the right. Use arithmetic shift.
Solution:
We copy the left-most bit and re-insert it from the left side and shift the rest to the right discarding the right-most bit:
 |
return top
Problem 3: shift the binary bits 10010111 to the right. Use logical shift.
Solution:
we insert a ‘0’ bit from the left and move the other bits to the right. The right-most bit will be dropped or discarded.
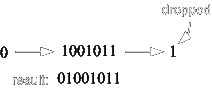 |
“ Note: rotating to the right is the same as logical shifting to the right. ”
return top
Logic Gates Problems
Problem 1: draw a logic circuit which is represented by the Boolean expression:
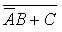 |
Solution:
The expression can be modified but it won’t simplify the circuit. So we use the given expression to generate our logic circuit like below.
The expression says: the complement of A is AND-ed with B. The result of this AND-ing is then OR-ed with C and then the whole expression is complemented. The circuit below represents the Boolean expression.
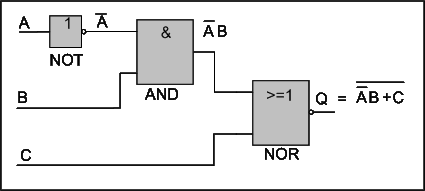 |
return top
Problem 2: simplify the circuit below:
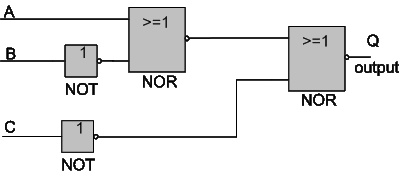 |
Solution:
We first develop the Boolean expression from the circuit like Q below:
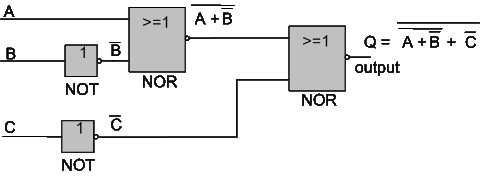 |
Now we can simplify the Boolean expression:
 |
Now we can redraw the circuit based on the new Boolean expression:
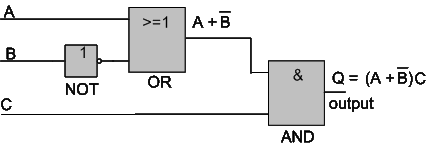 |
return top